© 2021 Daicel Corporation. ALL RIGHTS RESERVED.

メールマガジン
[Vol.090 2024年12月号]
Mail Magazine

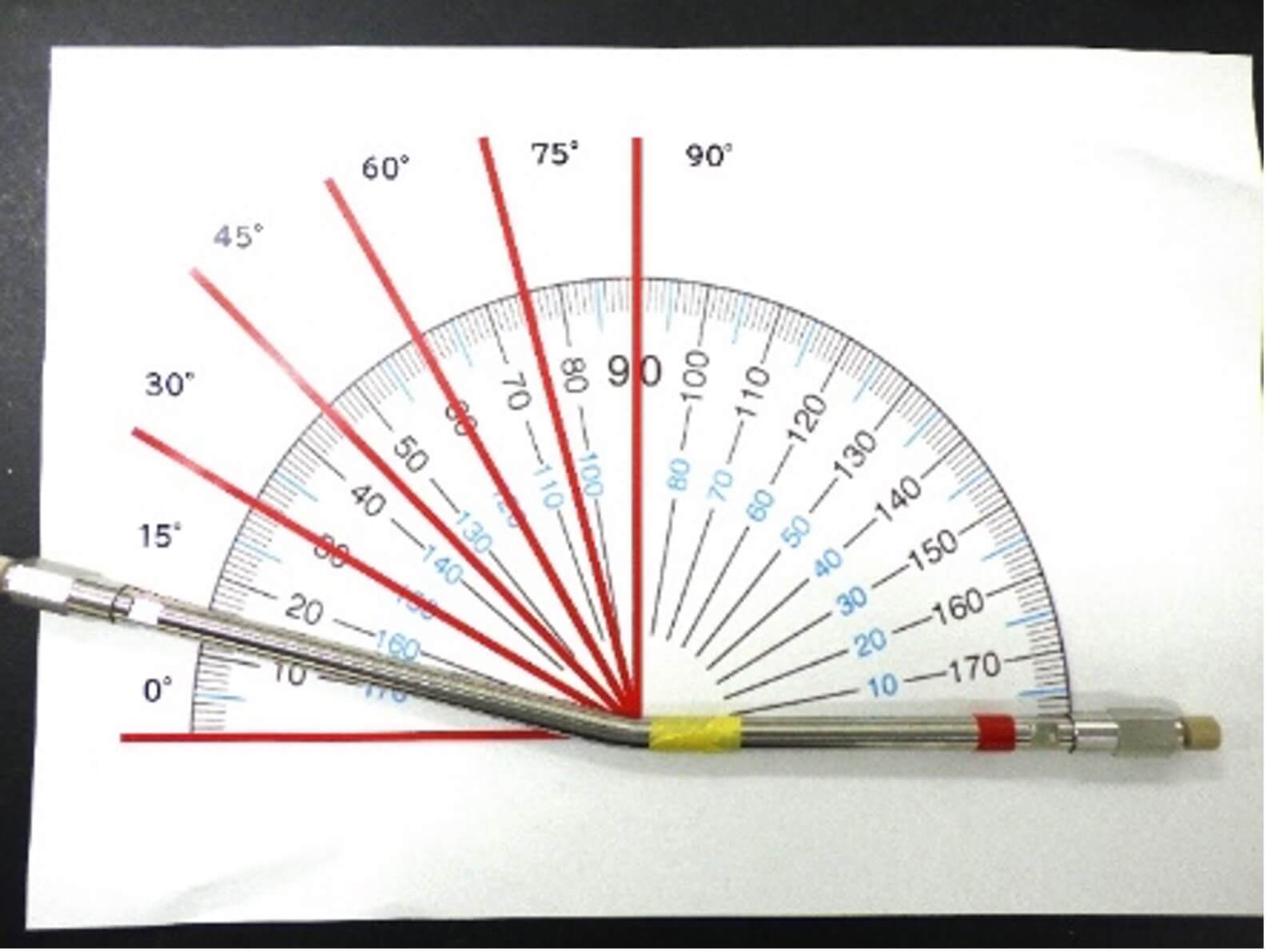
今回、匿名希望様から「良いマネ」でチャレンジしてください、と頂いたリクエストは、なかなか刺激的なもの-“カラムをU字やS字に曲げたら、ピークはどうなりますか?”―でした。 “そこそこ肉厚のSUS製分析カラム(0.46φ)は容易に曲げられないし、ちょっとこれは無理なチャレンジか…” と思っていたのですが、とある人から、“チューブベンター”なるものがあって、分析用カラムくらい折り曲げられますよ、との悪魔の囁きを耳にし、ついにはチューブベンター(8mm用) (写真①)をわざわざ購入して、折り曲げることにしました。でも、さすがにU字、S字は難しいので、45度にキラルカラムくんを折り曲げ(写真②)、ピーク形状がどんな風になるか、調べることとしました。
今回は、“分析用キラルカラムを折り曲げたら、ピーク形状にどんな影響を及ぼすか?”という、まあ…良い子も良くない子のどちらも、まともな神経の技術者・研究者ならば絶対やらないようなマネにチャレンジしてみました。


今回試験に使ったカラムは “CHIRALPAK® IB N-5” (0.46 cm I.D. x 15 cmL)です。では、どんなチャレンジ(実験)をしたか? はい、内容は簡単です。5度、15度、30度、最後は45度とキラルカラムを折り曲げ、そのたびに性能評価を行いました。勿体つけたタイトルの割に、超シンプルな実験検証で申し訳ありませんね。
まずは恒例の試験開始前の初期性能評価です。カラムクロマトグラムとその横にクロマトパラメーター[保持時間(t)、保持係数(k’)、分離係数(α)、分離度(R)、理論段数(N)、ピーク対称性(Ps)、カラム圧力をお示しします。
【HPLC評価条件】
カラム:CHIRALPAK® IB N-5 (0.46cmI.D. x 25cmL)
移動相:n-Hex/IPA = 90/10 <v/v>
流速:1.0 mL/min.
検出:UV254 nm
温度:25℃
評価サンプル:trans-Stilbene oxide (TSO)
打込み:1.0 mg/mL(移動相) x 5 mL
コンディショニング:25分

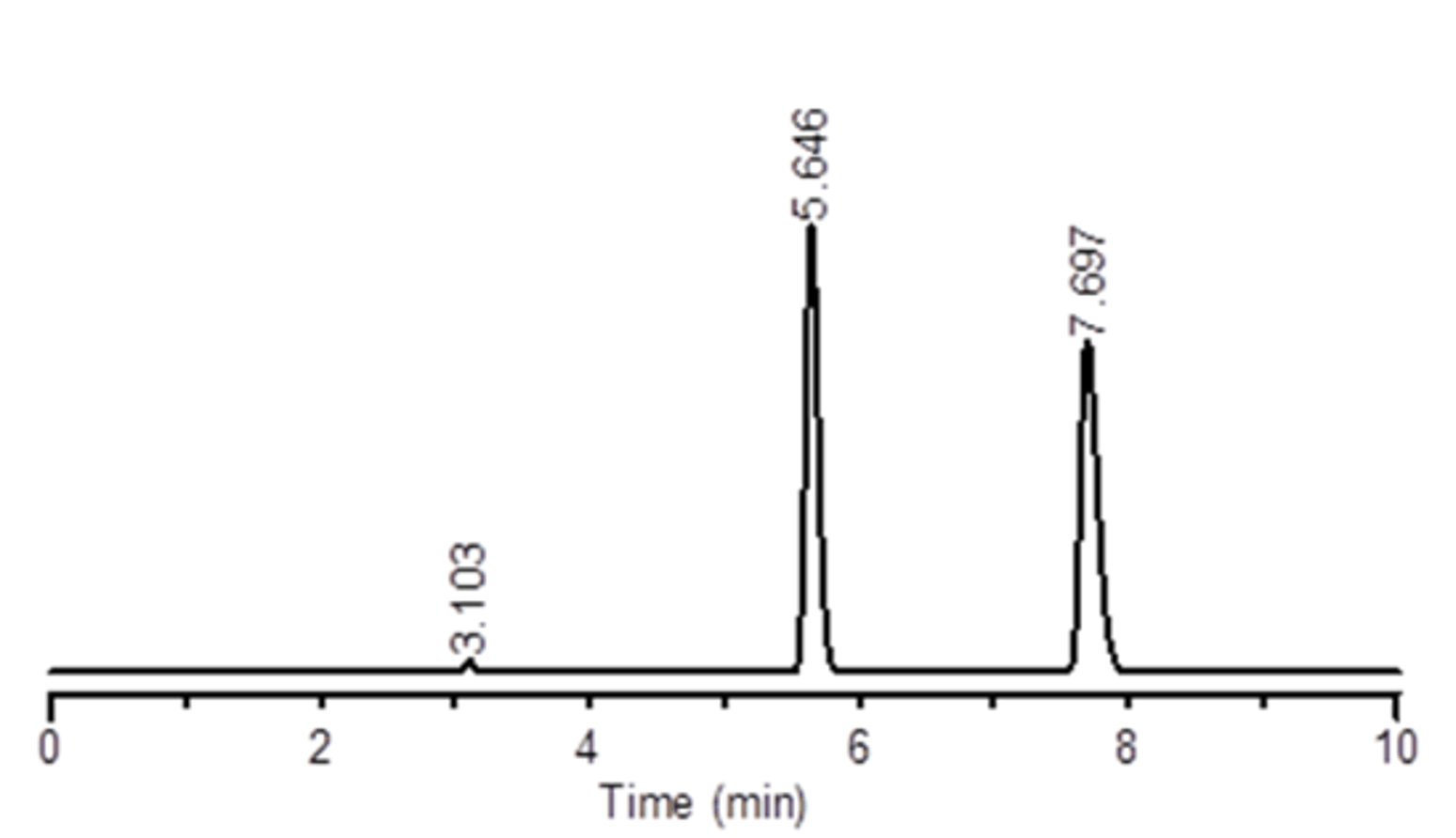
t1:5.65, t2:7.67
k’1:0.82, k’2:1.48
α:1.81, R:10.13
N1:17,367, N2:17,205
Ps1:1.20, Ps2:1.40
Press.:3.1 MPa
さて、折り曲げたときのそれぞれの写真③~⑥、クロマトグラムおよびクロマトパラメータ(保持時間(t)、保持係数(k’)、分離係数(α)、分離度(R)、理論段数(N)、ピーク対称性(Ps)、カラム圧力(システム圧力込み、Press.)の結果をお示しします。

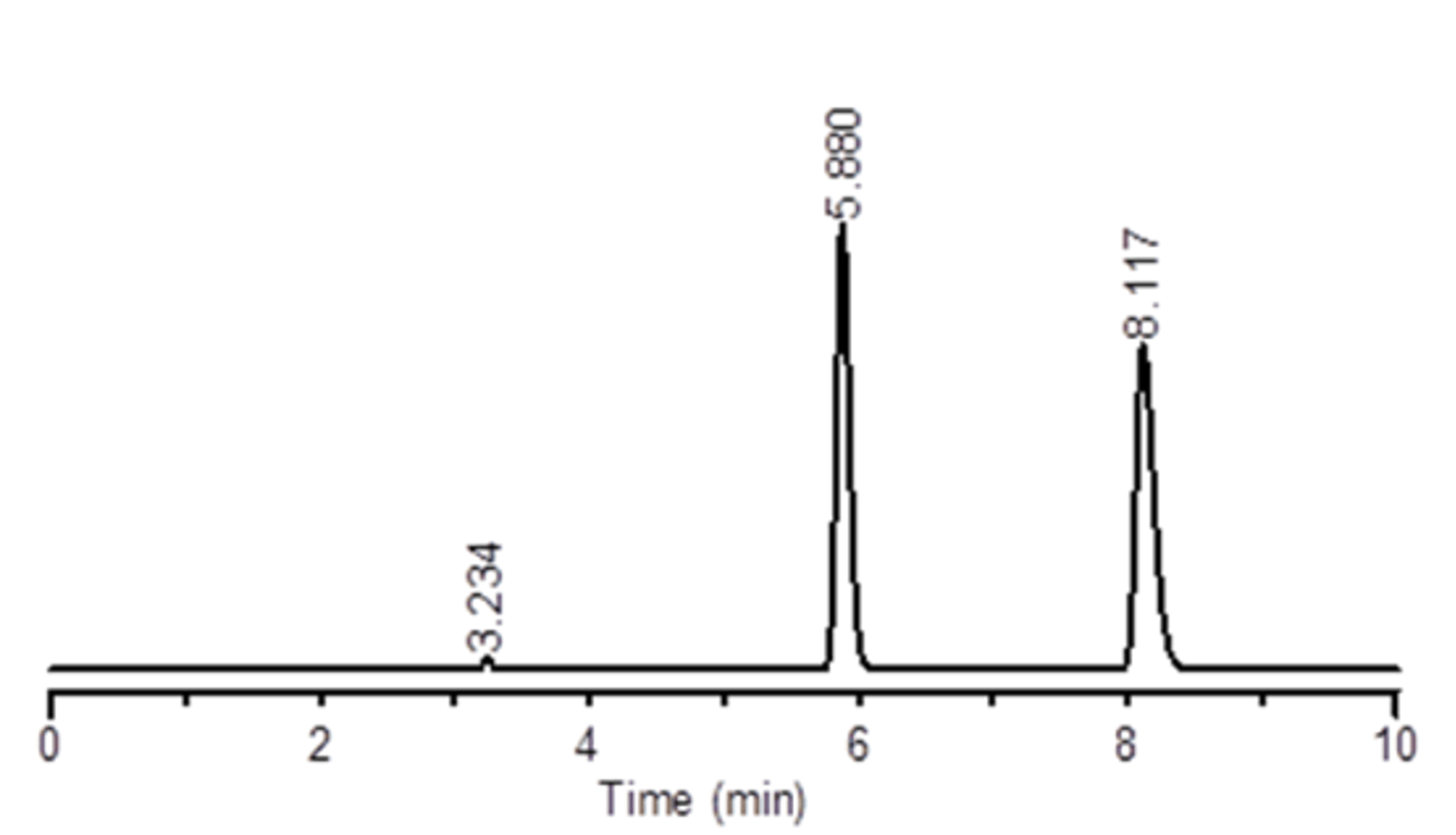
t1:5.88, t2:8.12.
k’1:0.82, k’2:1.51
α:1.85, R:10.55
N1:17,417, N2:17,299
Ps1:1.21, Ps2:1.41
Press.:3.0 MPa
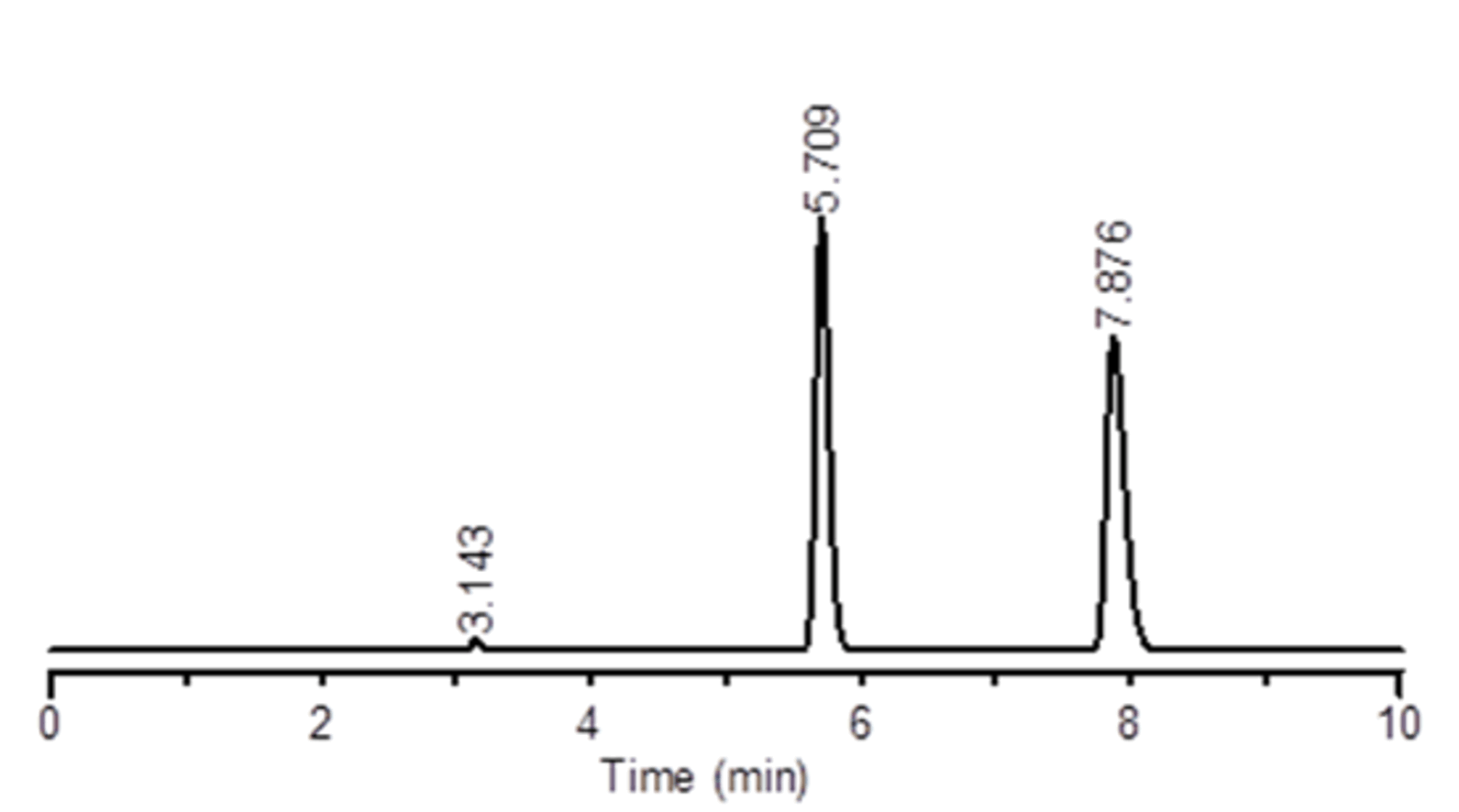
t1:5.71, t2:7.88
k’1:0.82, k’2:1.51
α:1.84, R:10.15
N1:16,311, N2:15,950
Ps1:1.22, Ps2:1.40
Press.:3.1MPa


t1:5.66, t2:7.81
k’1:0.82, k’2:1.51
α:1.84, R:9.12
N1:13,338, N2:12,747
Ps1:26, Ps2:1.41
Press.:3.1 MPa
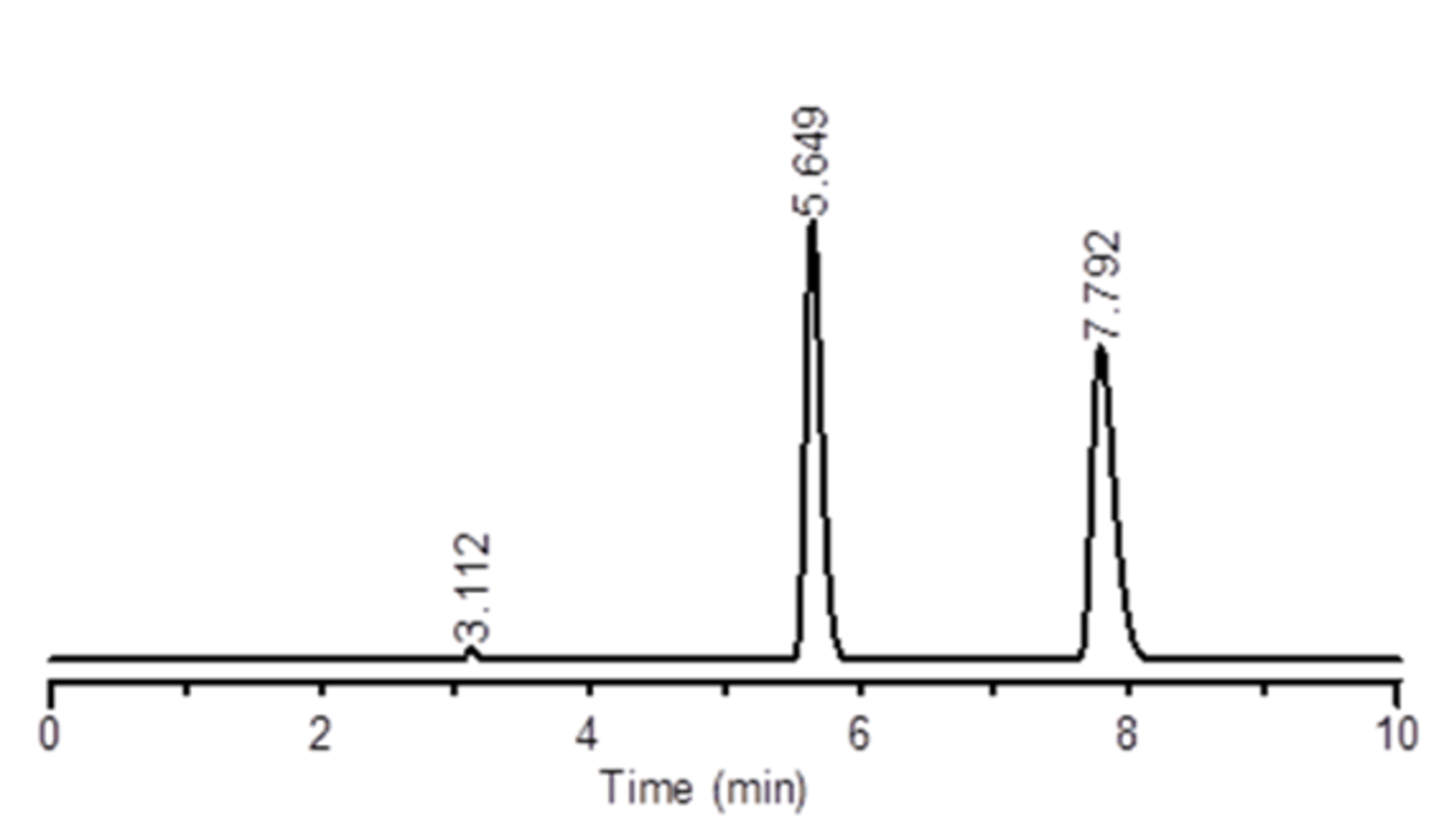
t1:5.65, t2:7.79
k’1:0.82, k’2:1.50
α:1.84, R:8.17
N1:10.876, N2:10.135
Ps1:33, Ps2:1.48
Press.:8.17
次にカラム折り曲げが最も影響を与えそうな、カラム理論段数、ピーク対称性の0度から45度までの推移のグラフをお示しします。
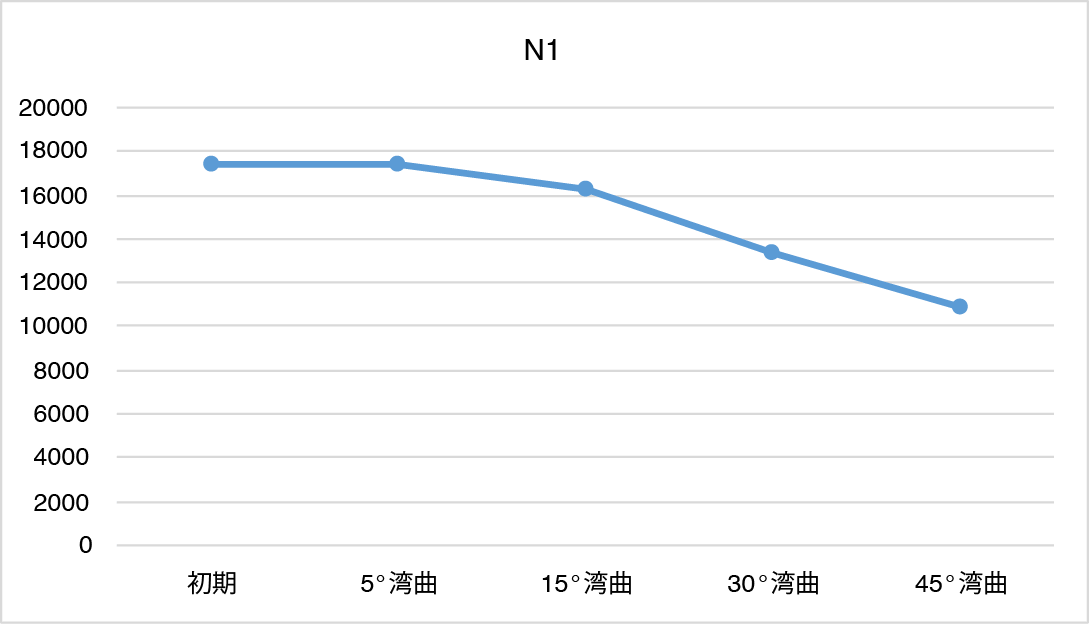
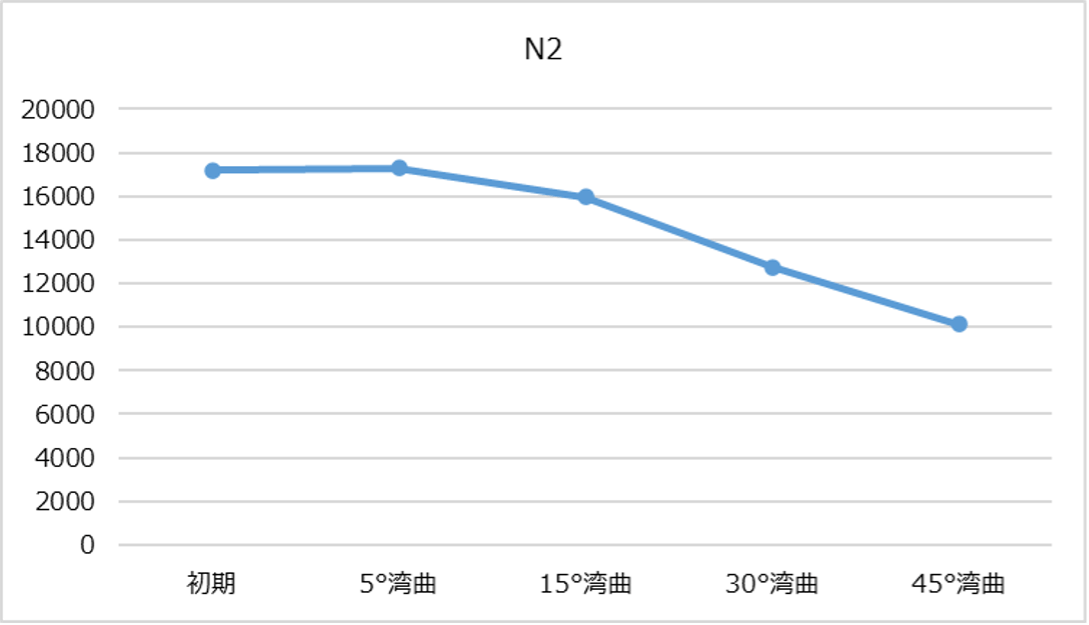
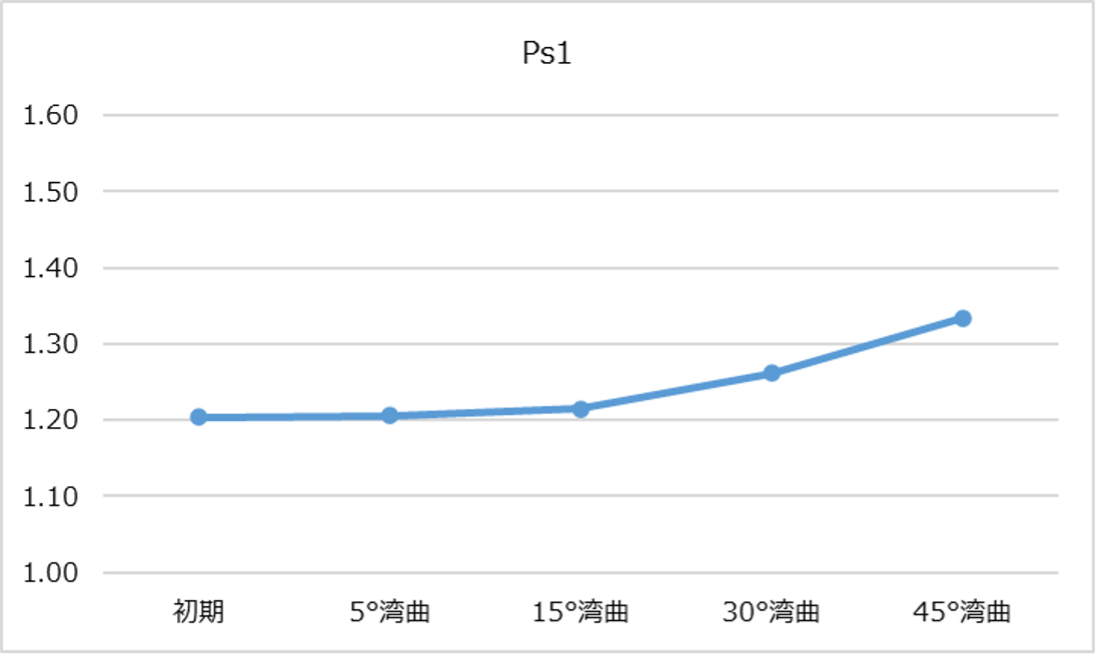
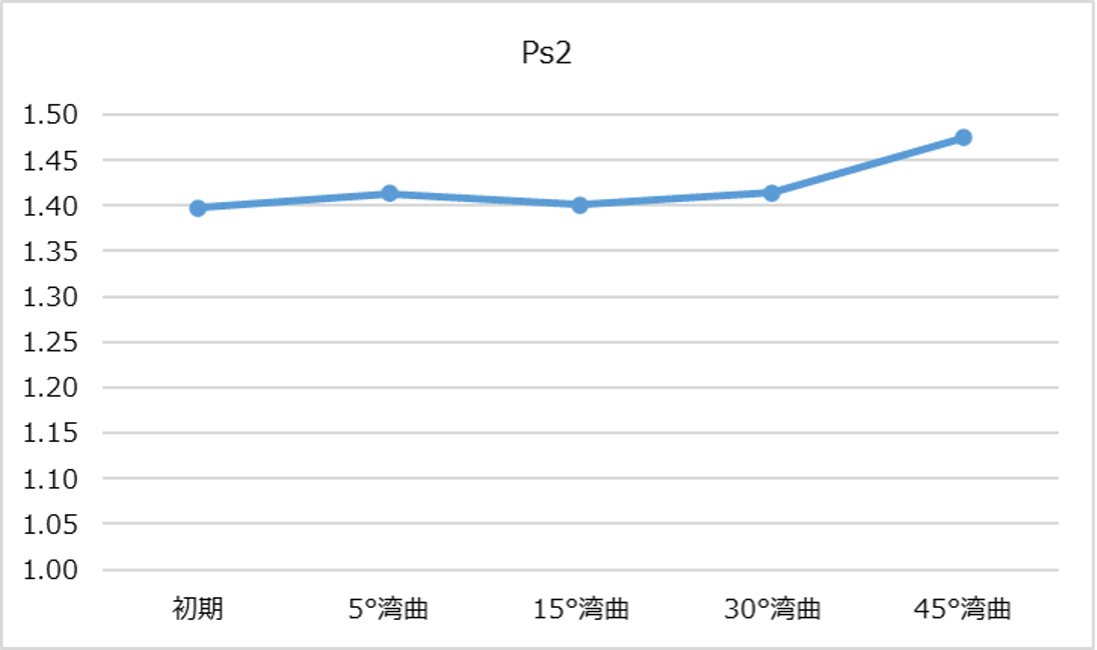
見事なくらいカラム理論段数が低下しました。45度折り曲げカラムでは、試験前カラムの理論段数の約7から6割にまで下がってしまいました。同時に、ピーク対称性の数値は上昇傾向、すなわちピークテーリング傾向にあり、最終的に5~10%大きくなりました。
そりゃ、こんなにひん曲がってしまったら、段数も落ちるでしょう、ピーク対称性も悪くなるでしょう、なのですが、ひょっとしたら、折り曲げたことで、内側(内周側)と外側(外周側)を通過する試料に距離の差(陸上競技のトラックをご想像ください)が出来たことで、外側を通過する溶質の溶出時間若干、遅くなることでピークテーリングが生じたのでは? と、さすが元・陸上競技部、部員(種目:短距離)ならではの発想(妄想)から、ちょこっと計算(①~③)をしてみました。
-
① 折り曲げをRと仮定して、R=45度の円弧(折り曲げでなく円弧と仮定)の長さが、カラム長さ=250mmとしました。
π:パイ(円周率)、r:円弧半径
2πr×45/360=πr/4=250mm
これをカラム内周側の弧の長さと(あくまで)仮定しました。
また円弧の半径はr=1000/πとなりました。 -
② 次にカラム径が4.6mmなので、半径が上記よりも4.6mm長い、すなわち(r+4.6)が半径である円弧の長さ:L(これが外周側長さ、折り曲げでカラム管が引き延ばされた、と仮定して)を計算してみました。
2π(r+4.6)×45/360=L(外周側円弧長さ) -
③ 次にL(外周側長さ)/250(内周側長さ)の比を計算するため、下式に①のr=1000πを代入しました
L/250=[π(r+4.6)/4]/[π(r)/4]
L/250=[π(1000/π+4.6)/4]/[π(1000/π)/4]=[(1000/π+4.6) ]/(1000/π)
ここで、π=3.14を代入してみましたら、L/250=1.014となり、外周側が内周側よりも1.4%長くなった計算結果になりました。
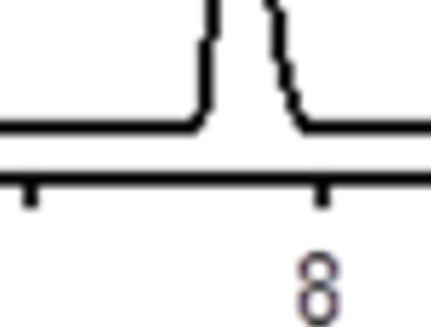
さて、ピークの広がりは、1.4%に近い値なのでしょうか?
ピーク幅:25.4秒
ピーク幅:31.3秒
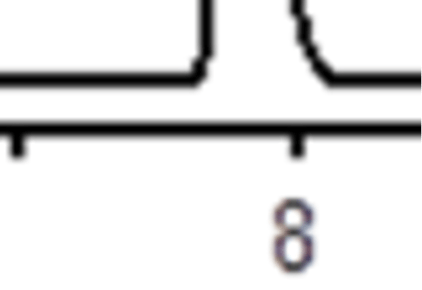
0度カラムと45度の折り曲げカラムの第二ピークのピーク幅の広がり(時間に換算)を比較したところ、23%も大きくなっていました。うむむ、ピークの広がりの程度が予想(妄想)と全然違う、ということで、単純にトラック競技の外周、内周の差で、ピークテーリングが起きたのではなくて、折り曲げられたことで充填層(状況)に何らかの甚大な影響が及んだことで、このような結果になったのだろう、と思われます、というか、そりゃ45度も曲げたらカラム管内部にも変形が起こって、カラム管中の充填層に何も起こらん訳ないでしょう、わざわざ分析カラムを折り曲げる道具まで買って、カラム折り曲げて、しかも余計な時間を使って、アホな計算までして… 一体、何をしているんだ、と言われそうです。
でも、“これが「良い子はマネしない」で企画の真髄です”、と胸を張って、正々堂々とお答えしたいと思います。ここまでお付き合い頂き、有難うございました。
★まとめ
かっこいいタイトルをつけて、良いマネ史上、もっとも過酷な試験を行ってみました。このご提案を頂きました匿名希望様に感謝申し上げます。この実験をしながら、頭をよぎったのは、昔、ユリ・ゲラーという人がスプーンを曲げると言っていたなあ、キラルカラムも曲がったのかなあ…、とか、“アップダウンクイズ”という昔のクイズ番組では、不正解だと滑り台の角度を徐々に上げ、最終的に滑り落ちなかった人が優勝、なんてTV番組があったなあ、などと、遠い昔に思いを馳せながら、楽しく実験をいたしました。
さすがに今回は、真似してみよう、という方はおられないと思うのですが、念のために言っておきます。
“(取説には記載していませんが)決してキラルカラムを折り曲げないでください”
どうかよろしくお願いいたします。
ファーマテックBU ライフサイエンス研究開発センター 所長 大西(あ)
協力:同・研究開発センター 元田
協力:ダイセル新井ケミカル、ファーマテック
生産開発課 木原
☆ダイセルの研究員がポスター優秀発表賞を受賞しました☆
2024年10月6~8日に、長野県諏訪市で行われました第35回クロマトグラフィー科学会議にて、弊社の研究員であり、金沢大学大学院自然科学研究科物質化学専攻の博士課程にも在籍しております元田秀樹さんが、ポスターでの研究発表を行い、みごと優秀発表賞を受賞いたしました!
ポスタータイトル:オリゴ核酸分野へのキラルカラムの適用
発表者:元田 秀樹、Mireille Schaeffer、Christophe Kientzy、永井 寛嗣、大西 崇文、Pilar Franco、大西 敦
内容:弊社の様々なキラルカラムを用いて、オリゴ核酸中に由来する異性体や不純物を分離分析できる条件を探索しました。

元田さんからの受賞のコメント
「このような栄誉ある賞を受賞できて大変光栄に思います。今回発表したデータは日本国内のみならず、海外グループ会社とも協力して取得したものであり、グローバル一丸となって得たものであります。カラムクロマトグラフィー、特にキラルの分野においてリーディングカンパニーであることを胸に、今後もグローバルに有用かつ魅力的なデータ・情報を発信していけるよう邁進していきます。」
受賞写真(クロマトグラフィー科学会会長:浜瀬健司九州大学教授(左)、クロマトグラフィー科学会誌編集委員長:北川慎也名古屋工業大学教授(右)、元田秀樹(中央))
この発表では、弊社のキラルカラムが立体異性体だけでなく構造異性体、さらにはオリゴ核酸に代表される比較的分子量が大きい分子も分析が可能であることが示されました。
ポスターの内容にご興味をお持ちいただいた方は、ポスターのコピーもご提供出来ますので、ぜひお問い合わせください。
今後も弊社からの研究発表にご期待くださいませ!!
 ENGLISH
ENGLISH








